Simple telescope and astronomical telescope, Construction working, uses, ray diagram
Simple telescope
A simple working telescope requires nothing more than a pair of lenses mounted in a tube. The lens in front, known as the objective, focuses an image; the lens in back, known as the eyepiece, magnifies the image. Although it may seem like a crude device, a simple telescope nicely illustrates the basic working principles of more powerful astronomical instruments.
LENSES
Light normally moves in straight lines, but there are situations in which this is not true. You are already familiar with some: for example, the distortions you see looking through the surface of the ocean occur because light bends as it passes from the water into the air. Long before we understood why light bends as it passes from one transparent material to another, people had used this effect to create lenses: optical devices which can gather light together or spread it apart.
In order to understand how a lens works, you need to know a little about how light behaves in passing from one material to another. Imagine a tank of water on the table in front of you; the surface of the water should be perfectly flat and horizontal. If you shine a ray of light straight down from above, it will pass through the surface of the water without bending. But if you shine the light in at an angle, it will bend as it passes through the surface. Fig. 1 illustrates two important facts about this effect. First, in passing from air to water, the light always bends into the water. Second, the smaller the angle between the light ray and the surface, the more it bends in passing through. The same rules would also apply if the tank of water was replaced with a block of glass.
To create a lens which can focus many parallel rays of light to a single point, the idea is to curve the surface of the glass so that all these rays, after passing through, come together at the same place. It’s a bit tricky to do this right, but we don’t need to worry about the details. The simplest kind of lens is a `plano-convex’ lens; one side is flat, while the other bulges out at the middle. Fig. 2 shows how such a lens focuses light. The optical axis of the lens is the thick line which passes right through the middle of the lens; a ray of light traveling along the optical axis is not bent at all. Rays which pass through the top of the lens are bent downward, while rays which pass through the bottom of the lens are bent upward. Thus all these light rays are bent toward the optical axis. If the lens is well-made, all rays meet at the same focal point. The distance between the lens and the focal point, measured along the optical axis, is called the focal length.
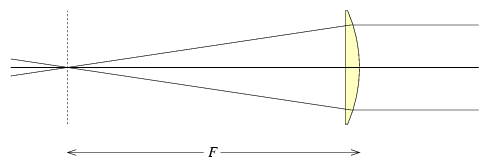
A simple lens in operation. Parallel light rays come from the right, pass through the lens, and meet at the focal point on the left. The thick line through the middle of the lens is the optical axis; the distance F is the focal length.
Image formation
A lens which could only focus light rays striking the glass head-on (as in Fig. 2) would be fairly useless for astronomy. Fortunately, most lenses can also accept rays which come in at a slight angle to the optical axis, and bring them to a focus as well. This focal point is not the same as the focal point for rays which are parallel to the optical axis; depending on the angle of the incoming rays, their focus lies on one side or the other of the optical axis, as shown in figure. But if the lens is well-made, all these focal points will lie on a plane which is parallel to the face of the lens; this is called the focal plane.
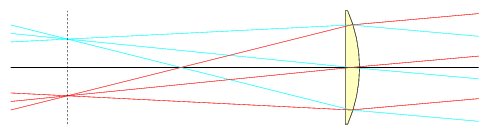
A simple lens forming an image. The red rays arrive with an downward slant, and come to a focus below the optical axis, while the blue rays arrive with a upward slant, and come to a focus above the optical axis. The vertical dotted line at left represents the focal plane.
There’s one slightly subtle consequence of this image-formation process: the image is upside-down! Fig. 4 shows why: rays from the lower part of the subject (on the right) come together at the upper part of the image (left), and vice versa. This is also true of a camera; of course, you turn the prints right way up when you get them back from the store, so you’re probably not aware that the image is upside down inside your camera.

The image formed by a simple lens is upside-down with respect to the subject. Here the subject (right) is an arrow with a red tip pointing upward; its image (left, at the focal plane) points down.
EYEPIECES AND MAGNIFICATION
To make a telescope you can actually look through, you’ll need to add another lens. This eyepiece lens magnifies the image formed by the large objective lens and directs the light to your eye. Basically, the eyepiece works a lot like a magnifying glass; it enables your eye to focus much more closely than it normally can. The eyepiece on a typical telescope allows you to inspect the image formed by the objective lens from a distance of an inch or less. Fig. 5 shows how the objective lens and eyepiece work together in a simple telescope.
The magnification of a telescope is easy to calculate once you know the focal lengths F and f of the objective lens and eyepiece, respectively. The formula for the magnification M is
M = F ÷ f
Here you can use any units for F and f, as long as you use the same units for both. For example, if you measure F in millimeters, you should also measure f in millimeters. Using the values for F and f you measured above, calculate the expected magnification of your telescope.
To measure the magnification of your telescope directly, we will set up a target – basically a picture of a ruler with marks a unit distance apart. From the other end of the room, focus your telescope on the target. Now look through the telescope while keeping both eyes open; you should see a double image, where one image is magnified and the other is not. Compare the two images; how many of the unmagnified units fit within one magnified unit? The answer is a direct measurement of your telescope’s magnification; record it in your notebook and compare it to the magnification you calculated using the formula above.
Astronomical telescope
An astronomical telescope is an optical instrument which is used to see the magnified image of distant heavenly bodies like stars, planets, satellites and galaxies etc. The final image formed by an astronomical telescope is always virtual, inverted and magnified.
Principle of Astronomical Telescope
An astronomical telescope works on the principle that when an object to be magnified is placed at a large distance from the objective lens of telescope, a virtual, inverted and magnified image of the object is formed at the least distance of distinct vision from the eye held close to the eye piece.
Construction of Astronomical Telescope
An astronomical telescope consists of two convex lenses : an objective lens O and an eye piece E. the focal length fo of the objective lens of astronomical telescope is large as compared to the focal length fe of the eye piece. And the aperture of objective lens O is large as compared to that of eye piece, so that it can receive more light from the distant object and form a bright image of the distant object. Both the objective lens and the eye piece are fitted at the free ends of two sliding tubes, at a suitable distance from each other.
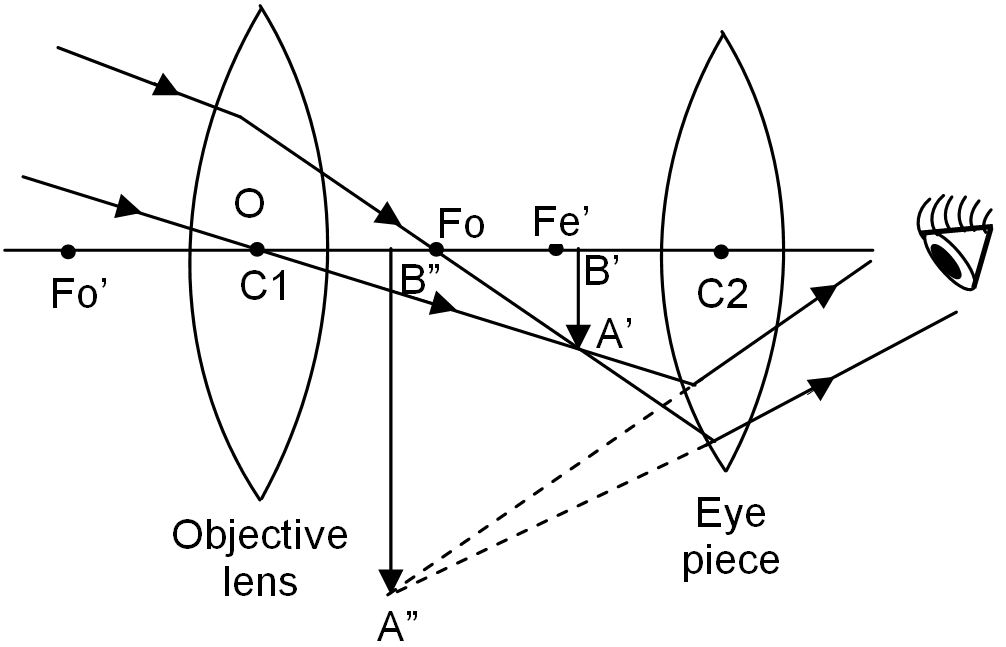
Working of Astronomical telescope
The ray diagram to show the working of the astronomical telescope is shown in figure. A parallel beam of light from a heavenly body such as stars, planets or satellites fall on the objective lens of the telescope. The objective lens forms a real, inverted and diminished image A’B’ of the heavenly body. This image (A’B’) now acts as an object for the eye piece E, whose position is adjusted so that the image lies between the focus fe’ and the optical centre C2 of the eye piece. Now the eye piece forms a virtual, inverted and highly magnified image of object at infinity. When the final image of an object is formed at infinity, the telescope is said to be in ‘normal adjustment’.
It should be noted that, the final image of object (such as stars, planets or satellites) formed by an astronomical telescope is always inverted with respect to the object. But it does not matter whether the image formed by an astronomical telescope is inverted or not, as all the heavenly bodies are usually spherical is shape.
Magnifying Power of an Astronomical Telescope
The Magnifying Power of a telescope is given by:
m = ![]()
Magnifying Power of an Astronomical Telescope
Where, fo = Focal length of the objective lens
fe = Focal length of the eye-piece lens
And the length (L) of the tube of telescope is equal to the sum of the focal lengths of the objective lens and the eye piece. Thus, L = fo + fe